【回帰分析で明確にする原因と結果の関係】#回帰分析 #原因 #結果 #Shorts

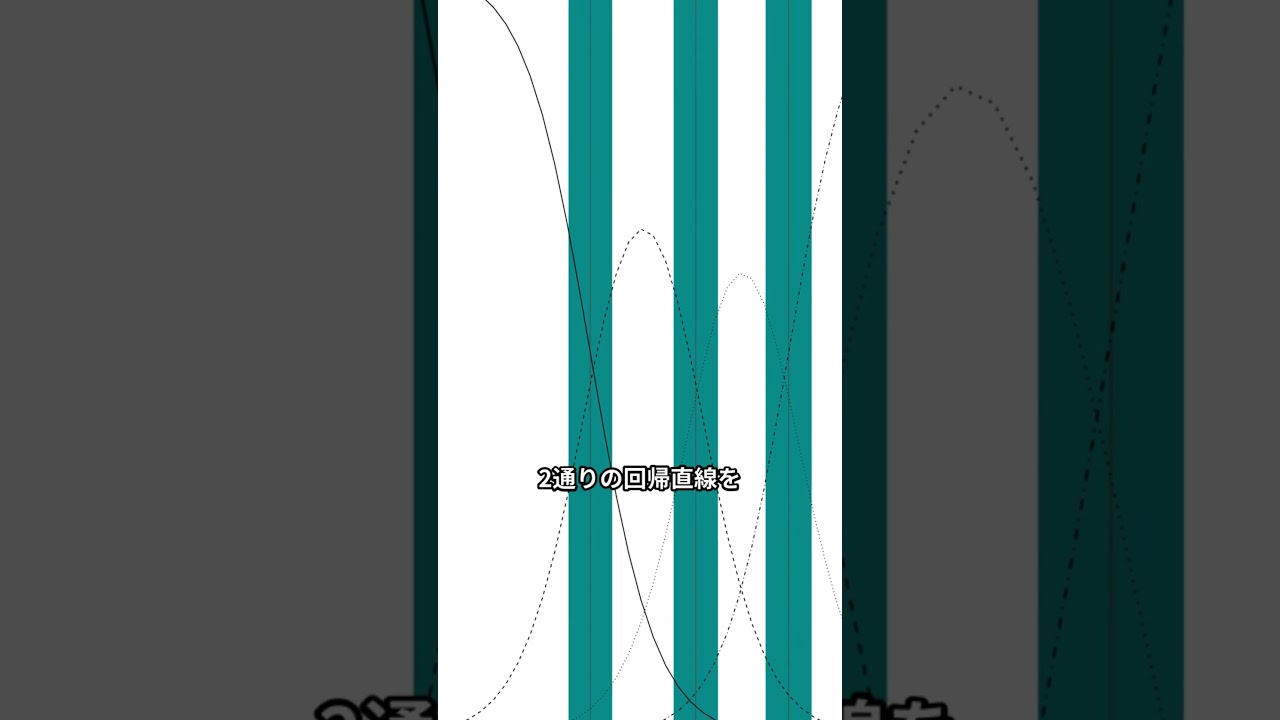
回帰分析では、原因と結果の関係を明確にすることが重要です。横軸に原因、縦軸に結果を設定し、回帰直線を描くことでその関係を示します。相関分析とは異なり、回帰分析では原因と結果の特定が前提となります。例えば、父親の身長が原因で息子の身長が結果とされます。実際に、グラフ上で回帰直線を2通り計算し縦横を逆にすると、2本の異なる直線が描けます。この現象は、楕円を縦横に切ってそれぞれ中点を結ぶ線を描く実験で確認できます。この2本の直線は一致せず、異なる角度で交差します。